Speeding-up homography estimation in resource-limited computing devices

A critical problem faced by computer vision on mobile devices is reducing the computational cost of algorithms and avoiding visual stalls. In this paper we introduce a procedure for reducing the number of samples required for fitting a homography to a set of noisy correspondences using a random sampling method. This is achieved by means of a geometric constraint that detects invalid minimal sets. In the experiments conducted we show that this constraint not only reduces the number of random samples at a negligible computational cost, but also balances the processor workload over time preventing visual stalls. In extreme situations of very large outlier proportion and noise level, it reduces in about one order of magnitude the number of required random samples.

We have modified the RANSAC Homography estimation to introduce a circular ordering constraint. We provide a version of the software that can be compiled and used in GNU/linux.

• Download the posters sequence.
• Download the posters squence image templates.
• Download the README.txt file
• Download a tar.gz file with the sample software
• Download the OpenCV 2.2 patch
• Download the OpenCV 2.4 patch
• Pull request accepted in OpenCV

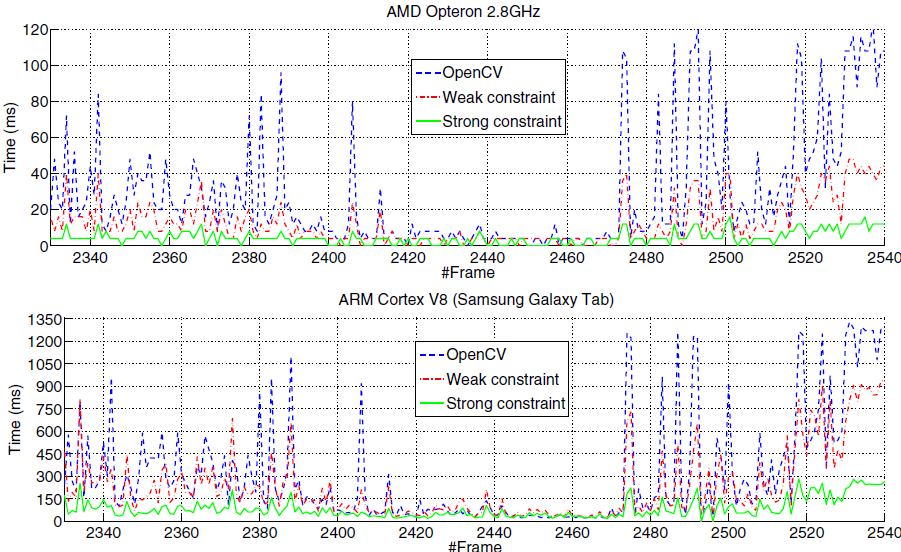
The code is minimal but it has a great impact in the speed of RANSAC homography estimation. And it could be important in CPU limited platforms like mobile devices. In a nutsell, RANSAC homography estimation time depends on the number of iterations and time needed to: 1) fit a homography H_i to a 4 points minimal set and 2) checking for inliers to H_i . However, if most of the random 4 points sets are not geometrically consistent then checking for inliers is not even necesary, they could be rejected very easily. The code has a heavy impact on estimation time mainly with a high number of outlier matches.

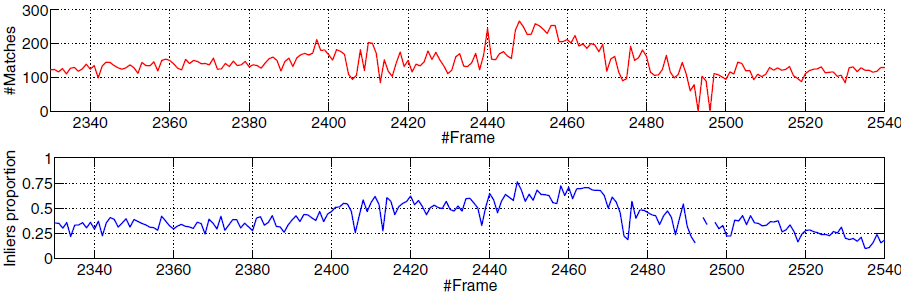
In the following figures we show the an example of homography estimation with and without the check: